Obtencion de las vistas de un objeto

 GENERALIDADES

          Se denominan vistas principales de un objeto, a las proyecciones ortogonales del mismo sobre 6 planos, dispuestos en forma de cubo. También se podría definir las vistas como, las proyecciones ortogonales de un objeto, según las distintas direcciones desde donde se mire.

          Las reglas a seguir para la representación de las vistas de un objeto, se recojen en la norma UNE 1-032-82, "Dibujos técnicos: Principios generales de representación", equivalente a la norma ISO 128-82.
 

          Si situamos un observador según las seis direcciones indicadas por las flechas, obtendríamos las seis vistas posibles de un objeto.

Estas vistas reciben las siguientes denominaciones: Vista A: Vista FRONTAL o alzado Vista B: Vista SUPERIOR o planta Vista C: Vista derecha o lateral derecha Vista D: Vista izquierda o lateral izquierda Vista E: Vista inferior Vista F: Vista posterior

 

 POSICIONES RELATIVAS DE LAS VISTAS

          Para la disposición de las diferentes vistas sobre el papel, se pueden utilizar dos variantes de proyección ortogonal de la misma importancia:

                    - El método de proyección del primer diedro, también denominado Europeo, DIN (antiguamente, método E)

                    - El método de proyección del tercer diedro, también denominado Americano, ASA (antiguamente, método A)

          En ambos métodos, el objeto se supone dispuesto dentro de un cubo con sus aristas transparentes, sobre cuyas seis caras, se realizarán las correspondientes proyecciones ortogonales del mismo.

          La diferencia radica en la posición del objeto y del plano de proyección que utilicemos, mientras en el sistema Europeo, el objeto se encuentra entre el observador y el plano de proyección, en el sistema Americano, es el plano de proyección el que se encuentra entre el observador y el objeto.

SISTEMA EUROPEO	SISTEMA AMERICANO
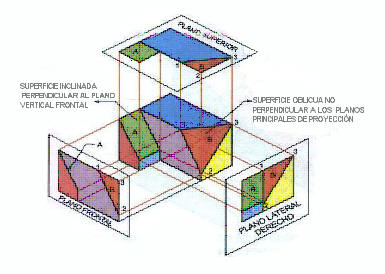Como podemos ver este diedro tiene superficies oblicuas (inclinadas), las cuales son las que tienen mayor dificultad por parte de los estudiantes de representar, los principios de la proyección del sistema diedrico, se aplican en la descripción de la forma de cualquier objeto material, sin tener en cuenta qué tipos de superficies lo forman. El tratamiento que se da a las proyecciones ortogonales de una superficie oblicua es similar al de superficies horizontales, verticales e inclinadas. Las superficies oblicuas e inclinadas se diferencian en su posición, con respecto a los planos de proyección, pues, mientras la superficie oblicua no es perpendicular a los planos principales de proyección, la superficie inclinada lo es a uno de ellos.           Una vez realizadas las seis proyecciones ortogonales sobre las caras del cubo, y manteniendo fija, la cara de la proyección frontal (A), se procede a obtener el desarrollo del cubo, que como puede apreciarse en las figuras, es diferente según el sistema utilizado. 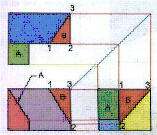                                                        La superficie inclinada A es perpendicular al plano frontal y se proyecta como una recta en la vista frontal, mientras que sus proyecciones superior y lateral derecha son rectángulos de distintos tamaños. la superficie B no es perpendicular a los planos de proyección y se proyecta, en las tres vistas, como triángulos de diferentes tamaños con sus lados unidos en un mismo orden Esta figura muestra las tres caras principales en el sistema ASA
SISTEMA EUROPEO	SISTEMA AMERICANO
El desarrollo del cubo de proyección, nos proporciona sobre un único plano de dibujo, las seis vistas principales de un objeto, en sus posiciones relativas.           Con el objeto de identificar, en que sistema se ha representado el objeto, se debe añadir el símbolo que se puede apreciar en las figuras, y que representa el alzado y vista lateral izquierda, de un cono truncado, en cada uno de los sistemas.
SISTEMA EUROPEO	SISTEMA AMERICANO

 RECUERDE QUE...

          Como se puede observar en las figuras anteriores, existe una correspondencia obligada entre las diferentes vistas. Así estarán relacionadas:

          a) En la vista frontal se identifica el ancho y el alto de la figura.
          b) En la vista superior se identifica el ancho y la profundidad.
          c) En la vista lateral derecha se identifica la profundidad y la altura de la figura.

          Habitualmente con tan solo tres vistas, el alzado, la planta y una vista lateral, queda perfectamente definida una pieza. Teniendo en cuenta las correspondencias anteriores, implicarían que dadas dos cualquiera de las vistas, se podría obtener la tercera, como puede apreciarse en la figura:

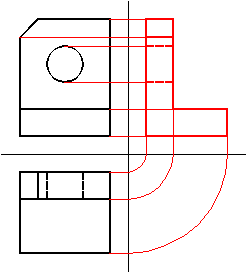
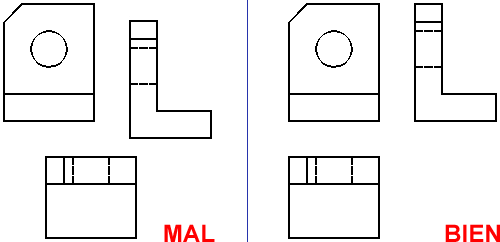
          También, de todo lo anterior, se deduce que las diferentes vistas no pueden situarse de forma arbitraria. Aunque las vistas aisladamente sean correctas, si no están correctamente situadas, no definirán la pieza.